Nájsť neznámu pravdu je náročné

 

Nemôžem nezačať takto. K názvu  ma podnietil materiál tlačová správa NKÚ SR: Žiť na dlh a bez vízie je nezodpovedné, chýba aktuálna stratégia riadenia dlhu či aj materiál MF SR Zdôvodnenie výšky hrubého dlhu SR a návrh opatrení na jeho zníženie a aj analýzy publikované v tlači a v TV. Čisté presné poznanie je obtiažne a zdĺhavé a práve to sa vzťahuje na dlh, jeho predvídanie a zdôvodnenie.

 

Človek je nedočkavý a zvedavý. Hovorí o tom aj dielo Kopernika. Jeho triumf bol triumfom čistého, matematického myslenia nad zmyslovým pozorovaním. Človek má túžbu a lásku k pravde doposiaľ nepoznanej. Chcem si pomôcť tým, že najskôr uvediem, čo rozumieme vedou, ktorá hľadá pravdu. Odpovedá nám na ňu filozofia: súhrn toho čo vieme, poznáme, čo je podľa dočasných prostriedkov a nástrojov čo najspoľahlivejšie a najbezpečnejšie zistené je veda.

K úvahe ma však priviedli aj priam povrchné debaty v NR SR či europarlamente a jednoduché ba priam prostoduché komentáre v tlači či TV. Ale aj dnešný boj o clá.

 

Nielen Koperník sa musel uchýliť k matematike. Náročná na ňu je aj ekonómia. Začnem D. Ricardom. Údajne vraj nedobytný prírodovedec kedysi požiadal Ricarda, otca ekonómie, aby mu pomenoval jedno ekonomické pravidlo, ktoré nie je ihneď zrejmé, ale pritom je veľmi dôležité. Bol to Ricardov „zákon pomernej výhody“, alebo doktrína komparatívnych nákladov. Dilema v zahraničnom obchode. Slobodný obchod  spôsobí, že všetky krajiny, ktoré sa ho zúčastnia budú mať benefit.

Ale politici sa nechcú riadiť týmto jeho rozborom. A preto máme dnes ekonomiky zamorené uvaľovaním kvót, colných taríf ba až obchodnými vojnami.

Jeho zákon komparatívnej výhody hovorí, že aj keď jedna krajina má absolútnu výhodu v pomere k druhej pri výrobe každého tovaru, hovorí sa, že má komparatívnu výhodu pri výrobe tovaru. Ricardo teda odhalil, že dve krajiny predsa môžu získať a to obchodom, ak je dokonca jedna krajina efektívnejšia ako druhá pri výrobe všetkých tovarov – teda, má absolútnu výhodu v každom tovare. V Ricardovej dobe majitelia pôdy v britskom parlamente chceli ochranu pred dovozom obilia z  Francúzska po napoleonských vojnách. Ale v parlamente sedeli aj príslušníci nastupujúcej buržoázie, noví podnikatelia (vzišli z priemyselnej revolúcie). Vzhľadom k tomu, že buržoázia najímala pracovné sily, dávala prednosť dostupnosti lacnejších potravín na trhu, aby nemuseli robotníkom platiť vyššie mzdy. Viac nájde čitateľ na internete.

 

Avšak v praxi má mimoriadny význam známa rovnica ohraničenia vládneho deficitu, čo požaduje NKÚ. Teda nadväzujem na úvod úvahy. Ide o vzťahy medzi príjmami z daní (T) a výdavkami vlády (G) vzhľadom na plynutie času. Toto verbálne nevyriešime. Obmedzím sa, aby som čitateľa uviedol do problému, iba na dve obdobia, teda

• hospodárstvom dnes (obdobie 1)
• hospodárstvom v budúcnosti (obdobie 2)

 

Nech v období 1 vláda má príjmy z daní T1 a výdavky vlády G1. V období dva bude mať príjmy z daní T2 a výdavky G2.. Uvažujme obe obdobia naraz. Musíme zistiť, ako sú zviazané príjmy a výdavky vlády za dve obdobia. Teda, vyjadrime si deficit vlády v prvom období ako rozdiel výdavkov a príjmov, čiže

 

D = G1 – T1                                 (4.48)

 

kde D je premenná deficit. Vláda vyfinancuje tento deficit tak, že predá obligácie vlády v rovnakej výške. V druhom období musí vláda získať príjmy z daní, ktoré splatia aj dlh, vrátane nárastu úrokov, a samozrejme vyplatiť aj svoje výdavky na nákup tovarov a služieb v druhom období. Ekonometricky

 

T2 = (1 + rD) + G2                        (4.49)

 

kde r je úroková miera.

 

Pre naše úvahy (neznámu pravdu) a vnímanie čitateľa, je dôležité odvodiť vzťah medzi príjmami z daní a výdavkami vlády na nákup tovarov a služieb v druhom období.

Dosadením (4.48) do (4.49) dostaneme

 

T2 = (1 + r) (G1 – T1)  + G2                 (4.50)

 

Z tohto vzťahu už vieme získať reláciu medzi príjmami vlády z prvého a druhého  obdobia a výdavkami vlády z prvého a druhého obdobia. Teda po úprave (4.50)

 

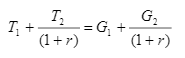                           (4.51)

 

Tento vzťah sa nazýva ohraničenie rozpočtu vlády. Jej význam je taký, že súčasná hodnota výdavkov vlády sa musí rovnať súčasnej hodnote príjmov z daní. Financie vlády by ju mali rešpektovať. Vidíme aj to, ako zmeny fiskálnej politiky, ktoré vláda robí dnes sú spojené so zmenami fiskálnej politiky v budúcnosti. Ak vláda zníži dane v prvom období bez zmeny výdavkov prvého obdobia, potom sa ženie do dlhu v druhom období voči tým, čo kúpili vládne obligácie. Tento dlh núti vládu vybrať si medzi redukciou výdavkov a zvýšením daní.

 

Teraz však ukážeme iný, pre tvorbu politiky dôležitý vzťah – správanie sa podielu dlhu a HDP daného hospodárstva. Žiada si to konštrukciu dynamického modelu rastu dlhu v národnom hospodárstve. Ekonomická teória pozná niekoľko takýchto modelov. Pre pochopenie tohto vývoja skonštruujeme model, ktorý bude nehomogénnou diferenciálnou rovnicou druhého stupňa s konštantným koeficientom.

Medzi dlhom vlády (D) a národným príjmom (HDP, Y) je vzťah. Tých vzťahov je viac. Uvažujme tieto bázické vzťahy medzi premennými  ekonomického systému (hospodárstva), model:

 

 

Zo (4.53) vidíme, že národný príjem rastie (prvá derivácia) konštantnou mierou rovnajúcou sa b za jednotku času a miera rastu národného dlhu  predstavuje fixnú proporciu z HDP, národného príjmu (rovnica 4.52). Tretia a štvrtá rovnica uvádzajú východiskové podmienky. Predpokladáme, že v každom čase je v hospodárstve konkrétna hodnota Y (hodnota Y(0) vo východiskovom roku) a konkrétna hodnota dlhu vo východiskovom roku – D(0).

Rovnica (4.52) je diferenciálnou rovnicou. Derivujme prvú rovnicu podľa času a po substitúcii z rovnice (4.53) dostaneme:

 

   

 

Výraz (4.56) je nehomgénna diferenciálna rovnica druhého rádu s konštantným koeficientom. Významný fakt, verbálne nezískateľný. Rovnicu môžeme riešiť, aby sme sa dozvedeli neznámy funkčný vzťah dlhu od parametrov a premenných, ktoré vystupujú v modeli (EÚ na to úplne zabudla). Riešme vzťah (4.56) dvojitým integrovaním. Najskôr integrujme (4.56).

Dostaneme:

 

 

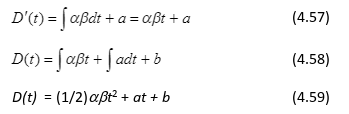
Získali sme všeobecnú rovnicu dlhu. Je to veľmi dôležitý ekonomický poznatok, založený na konkrétnych ekonometrických poznatkoch. Zabudujme do modelu (4.59) východiskovú podmienku, a to, že v čase 0 národný dlh dosiahol hodnotu D0:

 

D(0) = (1/2) ab(0) + a(0) +b                         (4.60)

takže

D0 = b                                                                (4.61)

 

Dosadením tejto hodnoty do (4.60) získame jeho konkrétnejšiu podobu:

 

D(t) = (1/2)abt2 + at + D0                                 (4.62)

 

Vystupuje v ňom ešte parameter a. Z rovnice (4.52) a (4.54) však zistíme, že

 

 

 

Po konečnom počte krokov získame funkciu vývoja dlhu a má tento tvar:

 

D(t) = (1/2)abt2 + aY0t+ D0                                  (4.66)

 

Pozrime si ešte funkciu podielu dlhu na HDP (požadujú to Maastrichtské kritériá). Z podmienok modelu sme sa dozvedeli, že dlh rastie kvadratickou funkciou. Z rovnice (4.53) modelu vieme vypočítať dráhu HDP. Konečné riešenie pre Y získame priamym integrovaním (4.53) a vložením počiatočnej podmienky (4.54).

Dostaneme:

 

Y(t) = bt + Y0                                                               (4.67)

 

Model sme úplne vyriešili a podstatu dráhy v čase premenných vieme vysvetliť. My sa však môžeme zaujímať o viac, lebo máme kritérium z Maastrichtského kritéria. Požaduje podiel dlhu na HDP. Aká je jeho dráha?

Dajme do pomeru D(t) a Y(t):

 

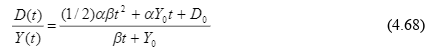
Z hľadiska toho, že chceme robiť analýzu je vhodné pravú stranu výrazu takto upraviť:

 

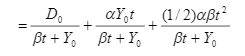                                          (4.69)

 

Ak t rastie do nekonečna, prvý zlomok sa blíži k nule, druhý zlomok sa blíži konštante a tretí zlomok rastie neohraničene (ide k plus nekonečno). Tieto výsledky získame ak vydelíme čitateľ aj menovateľ hodnotou t, čo nezmení hodnotu žiadneho zlomku. Náš záver je, že v tomto modeli rastie podiel dlhu na HDP bez ohraničenia, do nekonečna. Neznáma pravda: dlh prekročí hodnotu HDP po pár obdobiach. Takúto odpoveď nezískame iba verbálnou úvahou.

 

Za Maastrichtskými kritériami je neznalosť.

 

Nevedecké kritéria mali za následok zablúdenie ekonomík EÚ. Ako vidíme, môžeme experimentovať s parametrami v (4.52 a 4.53). Ďalšia analýza je v mojej knihe Makroekonomická analýza.

 

 

Záver

 

Človek je naozaj nedočkavý a zvedavý. Tak ako dielo Kopernika, jeho triumf bol triumfom čistého, matematického myslenia nad zmyslovým pozorovaním, tak ekonómovia potrebujú získať triumf nad ekonomikou, jej fungovaním. Človek má nástroje, teda ekonómovia majú bázický nástroj a to ekonometrický model. Teda, nájsť neznámu pravdu je náročné aj v ekonómii. Ale užitočné a potrebné. Kopernik ako prvý definoval aj  rovnicu množstva peňazí. I. Fisher, otec monetárnej teória až po ňom.

Dobre vieme, že clo má dve funkcie: predstavuje príjem štátneho rozpočtu, druhá colný protekcionizmus (ochrana domáceho trhu pred dovozmi zo zahraničia) a tým nepriamo aj ovplyvňovanie cenovej hladiny na colnom území. Poznatok sa dá odvodiť ekonometricky.

Nadpis úvahy platí tiež na problém colnej politiky. Zabudli sme na vedu a tak: German politicians furious at von der Leyen over new EU-US trade deal. (Nemeckí politici sú nahnevaní na von der Leyen-ovú za novú EÚ – USA zmluvu). Aj tu je  nájsť neznámu pravdu  náročné.

 

Riadenie z hlavy sa obráti v nechcené.

 

Prof. J. Husár

Bratislava 31/7/2025